Multiple Choice Markets
Manifold has released a new market mechanism for multiple choice predictions. This is the story of why and how we’ve developed it.
By James Grugett, Manifold cofounder
Why multiple choice?
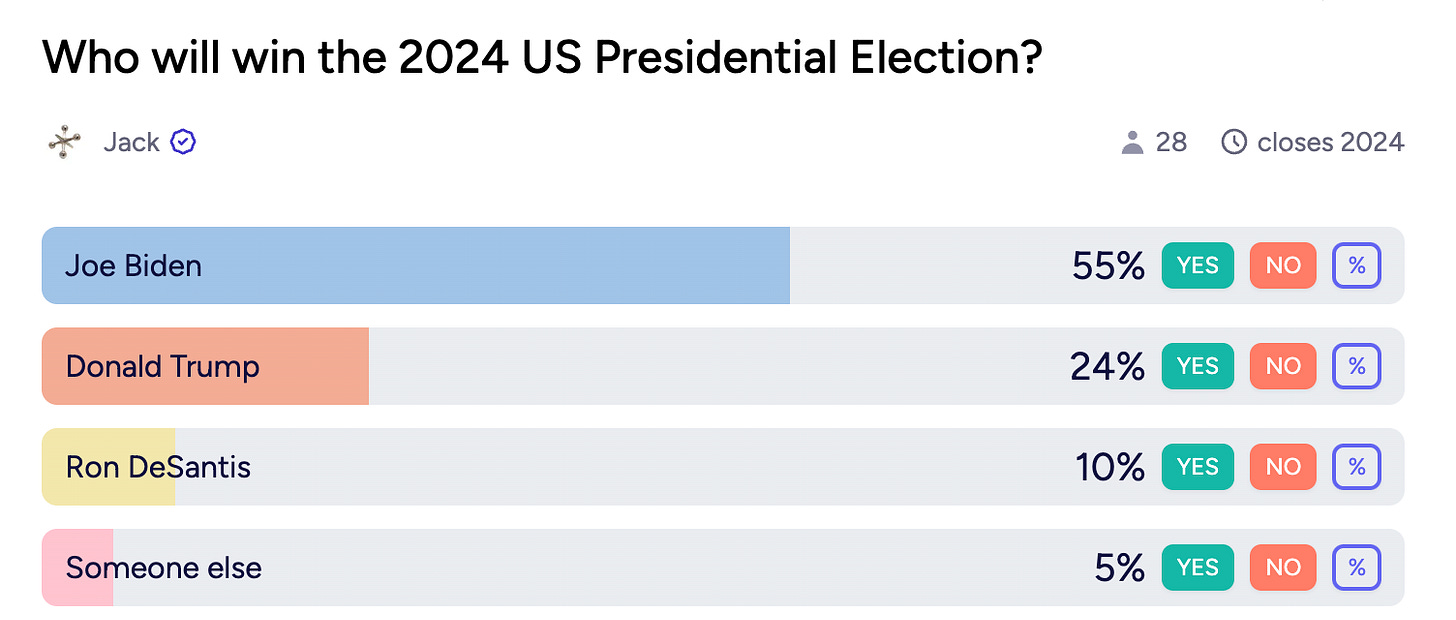
Prediction markets are typically phrased as Yes or No questions — like, “Will Joe Biden win the 2024 presidential election?”
But we discovered our users were creating many similar Yes/No markets substituting for one variable, which could be better phrased more as a general question:
Who will win the 2024 election? (Is it Biden, Trump, or DeSantis?)
When will SpaceX Starship reach space? (In Q1, Q2, Q3, or Q4?)
How much will the Fed raise interest rates? (Half a point? A quarter of a point?)
Rather than have these related questions implemented as many Yes/No questions scattered across many pages on our site, we can group them on one page for ease of access and comparison.
Better liquidity
But there’s also a logical relationship between many of these Yes/No markets. Typically, the options are mutually exclusive: only one person can win the election! That means, the probability of Yes for each of the options must sum to 100%.

Sites like PredictIt or Kalshi use independent Yes/No markets, which can leave the totals miscalibrated. PredictIt frequently has totals above 110% — that’s a problem!
But the bigger issue is not about percentages neatly adding up. It’s about failing to reuse liquidity between markets, which could help traders get the best price.
Manifold’s new multiple choice markets are the first to truly link the liquidity of Yes/No markets:
Limit orders on other options will be traded against when you bet
Likewise, the automated market maker (AMM) of every other option will be traded against when you bet
For example, if Alice places a limit order on Biden winning the 2024 election at 60% chance, then it could be matched when Bob bets on Trump, even though they are represented by independent Yes/No market mechanisms under the hood. The automated market maker for Biden would also be traded against when Bob bets on Trump.
The solution for linking the liquidity of individual Yes/No markets is to perform just-in-time arbitrage.
Simple arbitrage—how hard can it be?
If you’re buying Yes shares of Biden, that increases Biden’s probability. But to make sure the end probability still sums to 100%, we need to buy some No shares of every other option, to lower each other option’s probability just a smidgen so the total works out.
One problem with this idea is that it would be confusing to get No shares of other options when you were buying Yes of Biden.
Another problem is deciding how much “No” to buy of each other option. There are many ways to get the probability to add to 100% — for example, you could spend relatively more to buy No on Trump. What’s the right ratio to spend between options?
Both of these problems are solved by thinking in terms of shares of each outcome.
For example, No shares in Trump is kind of like Yes shares in every other option. Because of the logical relationship of shares, we can convert between them!
With this idea we can also solve the first problem, by converting all the No shares we buy back into Yes shares of Biden, as the user wants.
So what are the share conversion rules? Let’s study these clever identities! Ready? (Or, feel free to skip down to “Numerical optimization”.)
Share identities
One Yes share in every option is equal to 1 mana
Because we know exactly one option will resolve Yes, and the 1 Yes share in that option will be worth 1 mana, no matter which option is chosen.
One No share in an option is equal to 1 Yes share in every other option
Because the 1 No share pays out 1 mana in exactly the cases as the Yes shares — when any other option is chosen.
We can execute a Biden No bet by making one No bet on Biden, and one Yes bet on every other option buying equal shares, such that the end probability sums to 100%.
At this point, we can use the second identity to convert all the Yes shares in every other option directly into No shares of Biden!
Great! This gives us a unique solution to the arbitrage problem, which makes it seem like we are on the right track.
Exercise for the reader: Use the above two identities to turn 1 No share in each of first n-1 options into Yes shares of the last option plus mana. This conversion is needed when the user buys Yes shares of an option! Check exercise answer here
Numerical optimization
Here’s where we hit a brick wall — there’s no simple formula for figuring out the precise bet amounts to buy the required shares of each option.
In fact, because Manifold employs both an automated market maker and an order book (of which we are among the first to ever do!), to make even a simple bet in a Yes/No market is no small procedure. You need to alternately fill the bet from the order book and the automated market maker to get the best price.
It turns out that our bet code was already doing an intense guess-and-check loop to fill just the right amount.
With Multiple Choice, we’re adding more layers that we need to numerically solve for. This multiplies the computation cost.
In a prototype that I made during a hackathon last December, I ended up with three nested guess-and-check layers (using binary search) that locked up our web UI for a full second just to do the arbitrage between 4 options! It was clear this mechanism was not ready for production.
Closed-form solutions
A few months passed with this new multiple choice mechanism on the back burner.
Then, one day in February, a user submitted an issue on our open-source code base: He had found a closed-form equation that could replace one of our guess-and-check loops.

The solution allows us to calculate exactly how much mana should be spent to move to a given probability with our automated market maker. Fantastic!
With this, and one more similar missing closed-form solution (to calculate the amount of mana to buy a given number of shares), we could eliminate all but one of the costly numerical calculation loops.
Arbitrage on 4 options now takes only 3 milliseconds on my laptop running within the browser — nearly two orders of magnitude faster!
It’s shipped!
This new multiple choice mechanism is live, and 238 such markets have already been created on a variety of topics. Create your market here.
Having a good mechanism for multiple choice has been a holy grail for us.
We want creating a prediction market to be as easy as creating a Twitter poll. Writing options in natural language and adding as many options as you need is a big step forward compared to merely Yes or No questions.
Further, intelligently updating other options when you bet saves human attention — the mark of a good tool.
Lastly, I’m excited about the pure efficiency with how this mechanism maximizes liquidity by linking automated market makers on each option and allowing you to trade against users who placed limit orders on other options.
I hope this improved multiple choice market type enables more and better forecasts, increasing our collective knowledge.
Manifold Markets is like Wikipedia for the future. We curate knowledge from thousands of internet users and make it public and accessible. One day, we hope people will trust our markets (based on our growing track record) like they trust Wikipedia articles.
Next steps
This multiple choice mechanism could be foundational tech for more complex prediction market types.
Adding options
Next, we plan to let the market creator add new options while the market is ongoing.
Then, we can support “free response” markets, where users submit options that anyone can bet on. This concept was invented at Manifold and has been in production for a year with our Dynamic Parimutuel mechanism.
One area of research is supporting a special “Other” option that represents all options that have not yet been added. If a user owns shares of Other, then they could automatically gain the same number of shares in all new options when they are created.
Date range and numeric markets
Many markets on Manifold predict the date of when something will happen. This date range use case is mechanically similar to predicting a number, which is also popular.
Multiple choice works pretty well here already — you can bet on which month something will happen, or split a numeric question into buckets (0-10, 11-20, etc).
We could even generate the buckets for you to have more fine-grained predictions, however it becomes difficult for humans to bet on dozens of different buckets.
Cumulative numeric markets
Instead of buckets that split the probability space disjointly, traders often prefer betting on the cumulative distribution. For example, “Will this event happen before December?” is nicer to bet on than “Will this event happen in December?”
Here again, there is a logical relationship between these questions and with the right tricks, we may be able to support this framing with a derived mechanism of multiple choice.
Conditional markets
Consider the question, “If X wins the 2024 election, will the US enter a recession in the next 4 years?”, where X is a presidential candidate.
You can create Yes/No markets for different values of X today, but we know that only one of those markets will actually play out based on who wins the election. The rest get resolved N/A which undoes all the betting in those markets.
Knowing that only one of these markets will play out, we can allow you to spend the same amount of mana over and over in the market for each condition while only charging you once.
Creating native conditional markets with mutually exclusive options would thus allow greater capital efficiency.
Postscript
The mechanism presented here is actually our third major attempt at multiple choice! We’ve shipped a couple others to production before deciding we can do better.
The first was a generalization of Dynamic Parimutuel to n outcomes.
It had great liquidity properties, but does not guarantee fixed payouts. (You could buy shares at 50% and make as much profit as if you bought at 75%, for example.) There also was no obvious way to buy No on an option.
The second was a generalization of the binary Constant Product Market Maker to n outcomes.
This is, I think, the most obvious mechanism. However, it performs poorly when an option goes to an extreme probability (e.g. if the probability of Trump fell to < 1% chance) because, intuitively, it pulls liquidity there, and the rest of the liquidity is spread thin among the other options.
A second issue was that buying No in an option was not simple, and so it would be difficult to support limit orders (whereas we are reusing 95% of the Yes/No limit order code for our new multiple choice mechanism!).
Our Yes/No markets use a Constant Product Market Maker popularized by crypto applications such as Uniswap.
Note that we decided to fix p=0.5 for the multiple choice mechanism to make the math tractable. It also prevents liquidity issues when p becomes too large or too small. Lastly, the original justification for p was to allow adding liquidity efficiently without changing the probability. But we have solved that problem for multiple choice another way.
On liquidity: Users pay mana to create markets, which is put into a liquidity pool for the automated market maker (AMM). Normally, each 1 mana becomes 1 Yes and 1 No share inserted into the liquidity pool (another Share Identity).
However, for this multiple choice mechanism, we can do better! Because we know that only one option will resolve Yes, we can give out a larger number of Yes shares per option. This is another way the mechanism maximizes liquidity.
We solved a system of equations to determine the initial shares in each pool, if ante is the amount paid to initialize the multiple choice market of n options. The second equation is the CPMM equation for probability:
ante = poolYes + (n - 1) * poolNo1 / n = poolNo / (poolYes + poolNo)
Multiple choice resources



So, is it not possible to create markets with "write your own answer" anymore?